대충 살펴보자면 두가지 정도의 뜻이 있다.
1. 공대생의 행동/생활/사고 패턴을 희화화한 개그
2. 공대생이 아니면 이해 못하는 개그
[공대생이 제일 많이 하는 3가지 말]
1. 밥 먹었냐?
2. 레포트 썼냐?
3. 저 여자 예쁘다.
너무나 유명한 얘기라 한번씩은 다 들어봤으리라. 공대에 입학하고 반년만 지나면 이것이 웃기려고 지어낸 얘기가 아니라는 사실을 깨닫게 된다.
[공대생이 코끼리를 냉장고에 넣는 방법]
1. '코끼리'를 low pass filter에 통과시킨다. 그럼 '고기리'가 나온다.
2. '고기리'에 circular right shift 연산을 한다. 그럼 '리고기'가 된다.
3. '리고기'를 증폭률이 5인 op-amp에 통과시킨다. 그럼 '5리고기'가 된다.
4. 이제 오리고기를 냉장고에 넣는다.
[OOP적으로 돈버는 법]
상속.
[간미연 3행시]
간단히 말해서
미분 가능하면
연속이다
이정도는 공대생이 아니라 이과생이면 대개 이해 가능할 듯.
특이하게도 이 개그는 이해 못하는 경우가 2종류다.
1. 미분 연속성을 이해 못하는 경우
2. 간미연이 누군지 모르는 경우
[무제]
세상에는 10종류의 사람이 있다. 이진수를 이해하는 사람과 이해 못하는 사람.
이 촌철살인의 개그를 단번에 이해했다면 당신도 이미 공대생.
[공대생과 매트릭스]
1. 일반인의 대화
A : 매트릭스 봤냐?
B : 그럼! 키아누 리브스가 멋지고 컴퓨터 그래픽이 블라블라블라...
2. 공대생의 대화
A : 매트릭스 봤냐?
B : 헉! 거기도 시험범위냐?
1의 경우 매트릭스가 영화제목으로 해석된거고 2의 경우 매트릭스가 행렬로 해석된 경우.
3. 사타니스트의 대화
A : 매트릭스 봤냐?
B : 그럼. 그 매트릭스는 표상->존재->파괴->재표상을 반복하더군.
3의 경우 매트릭스가 모체로 해석된 것이다(www.obza.net의 left hand path참고).
[단어 장난]
Matrix reloaded : "선형대수학(수학과 학부과정에서 배우는 과목) 재수강"
"베르누이(역시 수학자, 베르누이 미분방정식과 베르누이 분포로 유명) 궁전"
"미션 임피던스(전자공학에 나오는 용어)"
위상수학 연구할때 먹는 카레는?
답=포앙카레(위상수학자)
[초코파이의 초코 함유량]
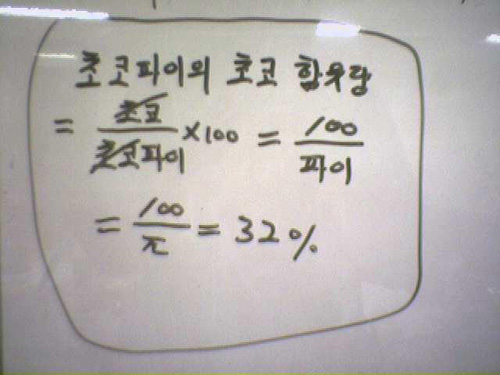

주의!
e=2.71828...인 초월무리수를 알고 있어야 이해가능. 이것은 자연로그함수의 밑이요 가우스 핵(gauss kernel)이나 익스포넌셜 함수(exponential function)에서도 밥 먹듯이 언급된다. 이 익스포넌셜 함수는 적분하든 미분하든 변하지 않는 천하무적함수이다.
[생명공학과 학생들의 대화중]
버스안에서 남녀가....
남> 너 생리했냐?
여> 아니 오늘 밤새워 준비해야되...
남> 그럼 내일 니꺼 복사좀 하자.
여> 다 되면 빌려줄께...
주위 사람들... 거의 경악을 넘어선 공포 수준...
어떤 사람은 혀끝을 차고, 한숨을 쉬고...
생명공학과 대학생 세포생리학 시험준비 중인데.....
생명공학과 학생이라면 누구나 한번쯤 경험이 있을것~
[즐 = 1.57]

[공대생 사고회로]
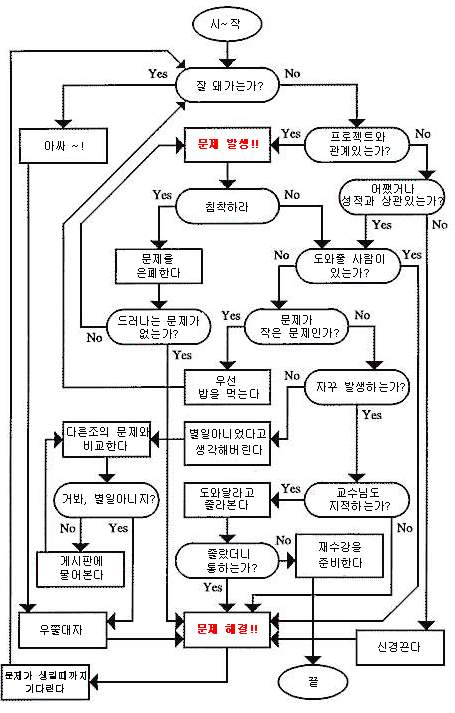
[TTL]
'TTL'이 몰까..?...
Twenty's Life 스무살의 자유...?...
전기회로나 전자회로를 본 사람이라면..아래와 같이 생각을
Transister Transister Logic....
정보통신쪽에서는 또다른 TTL(Time To Live)..이 존재..
Through-The-Lens 렌즈를 통과한 빛의 양을 재는 노출 방식..
[삶과 죽음의 동일성]
증명) 흔히 싸우다가 보면 '반죽여버린다'는 말을 쓴다.
반죽음 = 1/2 죽음 = 1/2 삶
양변에 2를 곱한다.
죽음=삶.
[여성은 언제까지 남자의 프로포즈를 튕길 수 있는가]
이 글은 확률과정론 및 랜덤변수이론을 알아야 이해가능한 개그이다.
상황 설정은 이러하다.
한 여성에게 100명의 남자가 순차적으로 프로포즈 한다고 하자.
100명 중 백마탄 왕자는 한명 뿐이고, 여성는 그 남자를 찾고 싶어한다.
물론 그가 첫번째로 프로포즈할지 100번째로 프로포즈를 해 올지는 알 수 없을
것이다.
여자가 100명의 남자 중 제일 멋진 남자를 고른다는 건 너무 불공평하니까
한번 프로포즈한 남자를 튕기면 다시는 그 남자는 선택할 수 없다고 하자.
즉 만약 더 나은 남자가 있을 거라는 기대감에 99명의 남자를 차례로 튕겨버렸다면
100번째 프로포즈하는 남자와 결혼하는 수 밖에 없다.
물론 첫번째 남자의 프로포즈를 받아드리면 99명의 남자가 어떤 남자인지 보지도
못한다.
그러면 여자에게는 전략이 필요하다.
<몇명까지는 일단 튕겨보고 그 다음부터 만나는 남자 중 제일 멋진 남자와
결혼하자.>
여자에게 몇명까지 튕겨보는게 가장 합리적인 전략이 될까?
조건부 확률을 생각해 볼 수 있다.
B : 여자가 백마탄 왕자를 정확하게 선택할 확률.
A1 : 백마탄 왕자가 첫번째로 프로포즈해올 확률.
A2 : 백마탄 왕자가 두번째로 프로포즈해올 확률.
.
.
.
A100 : 백마탄 왕자가 백번째로 프로포즈해올 확률.
그러면 여자가 백마탄 왕자를 정확하게 선택할 확률은 다음과 같이 표현된다.
P(B) = P(A1)*P(B/A1) + P(A2)*P(B/A2) + ... +P(A100)P(B/A100) ----(1)
이제 우리의 여성이 r명까지는 일단 튕겨보고
그 다음부터 만나는 남자 중 제일 멋진 남자와 결혼하기로 했다고 하자.
그러면 P(B/A1)=0, P(B/A2)=0, ..... , P(B/Ar)=0 이다.
(당연히...최초r명 안에 백마탄 왕자가 있었다면, r명까지는 튕기기로 한 여자의
작전은 완전...실패당.)
P(B/A(r+1))=1=r/r
(당연히 r+1번째로 백마탄 왕자가 프로포즈 해 왔다면 r명까지 튕긴 여자는 이전에
본 r명보다 더 멋진 남자를 바로 만나버린 거니까 백마탄 왕자 픽업할 확률은
100%?)
P(B/A(r+2))=r/(r+1)
P(B/A(r+3))=r/(r+2)
...
P(B/A(99))=r/99
P(B/A(100))=r/100
r+2번째에 백마탄 왕자가 있는데 r+1번째 프로포즈 한 남자가 이전에 튕긴 r명보다
나은 남자였다면, 여자는 최초세운 전략상 그냥 r+1번째 남자의 프로포즈를
받아들이게
되고 그러면 r+2번째 남자는 보지도 못하니까, 여자의 입장에서는 또 전략상
실패다.
따라서 r+2번째 남자(백마탄 왕자)의 프로포즈를 받기 위해서는 r+1번째 남자가
이미 튕겨보낸
r명보다 나은 남자여서는 안될 것이다. (^^;;;)
다시 말해
백마탄 왕자보다 앞서서 프로포즈 하는 남자중 가장 괜찮은 남자가
r번째이전(r번째 포함)에 여자에게 프로포즈를 하면 된다.
r+1번째에만 있지 않으면 된다. <-- 이 부분이 매우 중요하군요!
1,2,3,...,r,r+1번째 중 r+1번째만 아니면 되니까 확률은 r/(r+1)이다.
같은 방식으로 백마탄 왕자가 r+3번째로 프로포즈를 한다면
r+1번째 r+2번째에 여자가 프로포즈를 받아들여버리면 안된다.
그러려면 백마탄 왕자 이전의 남자들 중 가장 멋진 남자가
r번재 이전(r번째 포함)에 있으면 된다.
그러면 r+1번째, r+2번째 남자가 r번째까지의 남자보다 멋질 수 없으므로
여성는 r+3번째 남자가 어떤 남자인지 살필 기회를 갖게 된다.
확률은 r/(r+2)
이런 식으로 동일 한 풀이 과정을 거치면 백마탄 왕자가 백번째로 프로포즈 해올때
여자가 백번까지 기다려서 그 왕자를 선택할 확률은 r/100
이 결과를 (1)식에 대입하면
..100....1.......r
sigma --- * ---
..x=r..100.......x
이것이다! 드디어 r에 관한 함수가 나왔다.
항수가 많으니까 그냥 연속적으로 생각해서 적분을 하자.
.......................1.......r
integral r->100 --- * --- dx
......................100......x
...r.........100
= --- [lnx]
..100........r
어차피 우리는 위의 값을 최대로 만드는 r값을 찾는거니까, 그리고 상수항과
계수는
신경 안써도 되니까
d
--[ r{ln100} - r {ln r } ]= 0 을 만드는 r을 찾자.
dr
(답)
r = 37
답이 나왔다. 37명이다.
보통 한 여자에게 프로포즈하는 남자의 숫자가 10명이라고 하면
여자는 최초 3명까지는 튕겨볼 수 있어도 4명부터는 튕겨서는 안된다는 계산이
나온다.
그냥 괜찮다 싶으면 잡아야 된다는 것이다.
솔직히 10명도 많다.
보통 여성에게 프로포즈 하는 남자가 5명쯤 된다면 최초 한명 쯤은 공주병
환자처럼 튕겨볼 수 있으나
두번째 남자가 프로포즈해올 경우...
첫번째 남자보다 낫기만 하다면 프로포즈를 받아들여야 한다는 것이다. 그만
튕기고...
[공대생 테스트]
당신은 뼛속까지 공돌이가 아닌가요???
아니라구요???
그럼 다음 단어의 뜻은 무엇일까요?
probability
equation
evaluate
frequency
function
페이지를 넘기지 말고 잠시 생각을.
...
probability - 확률
equation - 방정식 등식
evaluate - 계산하다
frequency - 주파수
function - 함수
라고 생각하신분 그대는 뼛속까지 공돌이 =ㅅ=...
실제로 사전을 찾아보면
probability : 실제로 있음직함, 개연성, 일어남직함.
equation : 평균화, 동일화, 동등화, 균일화, 평형.
evaluate : 평가하다, 견적하다.
frequency : 자주 일어나기, 빈발, 빈번.
function : 기능, 작용, 효용, 직무, 구실.
억울하다구요?
그럼 "정의" 가 영어로 뭘까요
...
definition 이라고 생각한 당신은
역시나 공돌이=_=
justice 라고 생각하신 당신은 -
문돌이 -_-;
하나 더~~~~~
어디서 주워들은 이야기입니다...
그럼 다음 단어의 뜻은 무엇일까요?
critical function..
...
임계 함수?
라고 생각하신분 그대는 뼛속까지 공돌이 =ㅅ=...
사회과학쪽 전공 서적에서는.........
비판적인 기능...
[미분과 적분에 관련된 이야기 : 미분귀신 / 적분귀신]
옛날에 아주 아름답고 평온한 마을이 있었다.
그 마을의 이름은 자연수 마을. 즉 natural number village였다.
그런데 어느날 마을에 미분 귀신이 나타났다.
미분 귀신은 마을 사람들을 하나씩 미분시켜서 모조리 0으로 만들었다.
마을은 점점 황폐해가고 이를 보다 못한 촌장과 동네사람들이 반상회를 개최하였다.
몇 시간의 토론 끝에 이웃에 있는 방정식 마을에 구원을 요청하기로 하였다.
이웃마을의 소식을 들은 마을에서는 x^2장군을 자연수 마을에 급파하였다.
전투 시에 수시로 자신의 모습을 바꾸는 x^2장군 앞에서 잠시 당황한 미분귀신...
그러나 미분귀신은 잠시 생각하더니 3번의 미분을 통해서 간단히 해치우고 말았다.
그러자 방정식 마을에서는 x^3장군을 급파하였다.
그러나 그 역시 미분 귀신의 적수가 되기엔 역부족이었다.
단 4번의 미분에 그만 작살이 나고야 말았다.
당황한 방정식 마을에서는 x^n참모총장마저 보내는 초강수를 택하였으나
그 역시 n+1 번의 미분 앞에서 힘없이 무너지고 말았다.
이제 아무도 미분 귀신의 적수가 될 수 없으리라 생각했으나....
방정식 나라에는 마지막 희망 sinx,cosx 두 장군이 있었다.
좌 sinx, 우 cosx 장군이 미분 귀신과 전투를 시작하였다.
미분 귀신은 적잖이 당황하지 않을 수 없었다.
아무리 미분을 하여도 서로 모습만 바꿔가며 계속 덤비는
sinx, cosx 장군 앞에서 더 이상 싸울 힘이 없었다.
그러나 그 순간 미분 귀신은 꾀를 내어 cosx 장군을 미분시켜 sinx 장군에게 던져버린 것이다.
마지막 희망이었던 두 장군은 서로 부디쳐서 그만 자폭하고 말았다.
일이 이쯤 되자 방정식 마을에서는 용병을 구하느라 난리가 일고 있었다.
그런데 전설적인 용병이 등장하였다. 그의 이름은 바로 exponential 검신이었다.
그가 가진 e^x 라는 무기는 미분
귀신이 수백번의 미분을해도 전혀 손상되지 않았기 때문이다.
미분귀신은 당황하기 시작하였다.
이제 승리는 exponential의 것처럼 보였다.
하지만 끝내 그마저 미분 귀신에게 패하고 말았다.
글쎄....
그 미분귀신이...
y 로 편미분을 해버리고 말았던 것이다...
우리의 미분귀신이 exponential함수 e^x를 죽이고 미분에 싫증을 느낀 나머지 자연수 나라를 떠났다.
마침내 평화가 찾아온 자연수 나라.. 그러나, 아....! 평화란 지속될 수 없는가?
이번에는 이 나라에 적분귀신이 나타나 자연수들을 닥치는 대로 적분을 시작했다!
적분귀신은 자연수들을 적분해 쓸데없이 덩치를 키워버리는가 하면,
출처가 불분명한 C(적분상수)라는 것들을 대량으로 만들어내었고,
심지어는 x로 적분한뒤 다시 y로 적분해 xy라는 악질 돌연변이까지 만들어 내는 것이었다
이제야 평화가 오는가 했던 자연수 나라의 촌장은 아연실색을 하며
옆 마을 다항식의 나라에 도움을 청했다. 그러나 다항식의 나라는
적분귀신은 자국에 도움이 된다며 이를 거절했다. 심지어 '적분귀신을 환영합니다'
라는 플랭카드를 내걸기도 하였다. 자연수왕은 얼마 안 남은 순수 자연수들을 모아
대책회의를 열었다. 회의 결과 다시 미분귀신을 불러야 한다는 의견이 나왔다.
그러나 미분귀신을 부르면 그들조차 막대한 피해가 있기에 그들 사이에서도 의견이 분분했다.
결국 미분귀신을 부른 후 순수 자연수들만 비밀 아지트에 숨기로 하고 미분귀신을 불렀다.
다시 자연수 마을에 온 미분귀신..!
일단 상수 C들을 닥치는 대로 죽이고, 다항식들을 죽이기 시작했다.
거의 모든 다항식들이 죽어갈 무렵, 미분귀신 앞에 적분귀신이 나타났다.
적분귀신 "문제를 내어 이기는 쪽이 사라지도록 하자"
미분귀신 "좋다(흐흐.. 내겐 편미분이라는 무기가..)"
그.러.나...
적분귀신이 문제로 제시한 것은 무한다변수 다항식
Lim a1*a2*....*an 이었다.
n->∽
아무리 편미분을 해 봐도 끊임없이 쏟아지는 변수들..
미분귀신 "포기다.. 너의 솜씨를 보여다오..-_-;;"
적분귀신 "가소로운 것.. 에잇!"
눈앞의 무한다변수다항식이 흔적도 없이 소멸되어버리는 것이 아닌가...
미분귀신 "어.. 어떻게?-_-;;;"
적분귀신 "......."
그렇다...
적분귀신은 다항식을 0에서 0까지 정적분해 버렸던 것이다...
적분귀신은 정말 대단했다.
승승장구를 치던 적분귀신에게 대적할만한 상대가 자연수 마을에서는 더이상 존재하지 않았다.
여지없이 무너진 미분귀신은 함께 힘을 합하여 적분귀신을 물리칠 동지를 찾아 나섰다.
정수마을, 유리수마을, 실수마을, 심지어 그 복잡하다는 복소수(complex number)마을까지...
그러나 미분귀신은 더이상 동지를 찾을 수 없는듯 했다.
"수의 마을에서는 도저히 찾을 수 없는것인가?..."
자포자기한 미분귀신 앞에 펼쳐진 광경은 정말 놀라운 광경이었다.
실수 및 복소수 마을에서 continuous function들이
어떤 놈에게 여지없이 터져서는 산산 조각이 나는 것이었다.
"저놈이닷!" 미분귀신이 외쳤다.
자세히 보니 그놈은 delta function 였다.
연속함수들을 sampling을 통해 discrete function으로 만들고 있었던 것이다.
며칠 후...
자연수 마을로 돌아온 미분귀신은 델타함수를 적분귀신 앞에 내놓았다.
적분귀신은 자신의 비장의 무기인 0에서 0까지 정적분을 사용했다.
그러나 delta function은 사라지지 않고 1을 남겼다.
delta function은 정말 대단했다.
특이하게도 0(-0)에서 0(+0)까지 정적분을 하면 1이되는 것이었다.
순간 당황한 적분귀신은 정신을 가다듬고 다시 0에서 0까지 정적분을 시도했다.
그러자 1이 사라졌다.
이때 나선 미분귀신은 delta function을 무한번 미분해주기 시작했다.
적분귀신이 아무리 아무리 0에서 0까지 정적분을 시도해도
미분을 통해 계속 delta function의 변종들이 나타나는 것이었다.
적분귀신은 드디어 두손두발, 아니 두 인티그랄(integral)을 다 들고 말았다.
미분귀신과 delta function의 연합전선은 정말 대단했다.
그러나 잠시잠깐 그들이 한눈을 판 사이에
그들은 사라지고 말았다.
"무슨일이지...?" 적분귀신이 고개를 들었다.
...
...
...
그 거대한 못짓.
그는 말 한마디로 모든 것을 사라지게 할 수 있는
거의 신적인 존재였다.
그는 바로 '정의(definition)귀신'이었다.
미분귀신과 델타함수가 열심히 ally를 해도
마지막에 정의귀신이 "= 0" 한마디면 끝나는 것이었다.
과연 정의귀신을 대적할 자가 이세상에 존재할른지...
존재한다. 바로 정의귀신을 창조한 미분위상수학대박사. 그러나 정의귀신은 미분위상수학대박사에게 광신적으로 충성하기 때문에 서로 싸우는 일은 없다. 단지 미분위상수학대박사가 정의귀신보다 훨씬 전지전능함을 말하려는 목적에서 언급한 것이다.
1. 공대생의 행동/생활/사고 패턴을 희화화한 개그
2. 공대생이 아니면 이해 못하는 개그
[공대생이 제일 많이 하는 3가지 말]
1. 밥 먹었냐?
2. 레포트 썼냐?
3. 저 여자 예쁘다.
너무나 유명한 얘기라 한번씩은 다 들어봤으리라. 공대에 입학하고 반년만 지나면 이것이 웃기려고 지어낸 얘기가 아니라는 사실을 깨닫게 된다.
[공대생이 코끼리를 냉장고에 넣는 방법]
1. '코끼리'를 low pass filter에 통과시킨다. 그럼 '고기리'가 나온다.
2. '고기리'에 circular right shift 연산을 한다. 그럼 '리고기'가 된다.
3. '리고기'를 증폭률이 5인 op-amp에 통과시킨다. 그럼 '5리고기'가 된다.
4. 이제 오리고기를 냉장고에 넣는다.
[OOP적으로 돈버는 법]
상속.
[간미연 3행시]
간단히 말해서
미분 가능하면
연속이다
이정도는 공대생이 아니라 이과생이면 대개 이해 가능할 듯.
특이하게도 이 개그는 이해 못하는 경우가 2종류다.
1. 미분 연속성을 이해 못하는 경우
2. 간미연이 누군지 모르는 경우
[무제]
세상에는 10종류의 사람이 있다. 이진수를 이해하는 사람과 이해 못하는 사람.
이 촌철살인의 개그를 단번에 이해했다면 당신도 이미 공대생.
[공대생과 매트릭스]
1. 일반인의 대화
A : 매트릭스 봤냐?
B : 그럼! 키아누 리브스가 멋지고 컴퓨터 그래픽이 블라블라블라...
2. 공대생의 대화
A : 매트릭스 봤냐?
B : 헉! 거기도 시험범위냐?
1의 경우 매트릭스가 영화제목으로 해석된거고 2의 경우 매트릭스가 행렬로 해석된 경우.
3. 사타니스트의 대화
A : 매트릭스 봤냐?
B : 그럼. 그 매트릭스는 표상->존재->파괴->재표상을 반복하더군.
3의 경우 매트릭스가 모체로 해석된 것이다(www.obza.net의 left hand path참고).
[단어 장난]
Matrix reloaded : "선형대수학(수학과 학부과정에서 배우는 과목) 재수강"
"베르누이(역시 수학자, 베르누이 미분방정식과 베르누이 분포로 유명) 궁전"
"미션 임피던스(전자공학에 나오는 용어)"
위상수학 연구할때 먹는 카레는?
답=포앙카레(위상수학자)
[초코파이의 초코 함유량]
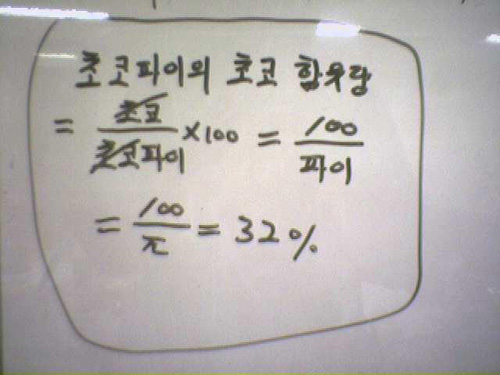

주의!
e=2.71828...인 초월무리수를 알고 있어야 이해가능. 이것은 자연로그함수의 밑이요 가우스 핵(gauss kernel)이나 익스포넌셜 함수(exponential function)에서도 밥 먹듯이 언급된다. 이 익스포넌셜 함수는 적분하든 미분하든 변하지 않는 천하무적함수이다.
[생명공학과 학생들의 대화중]
버스안에서 남녀가....
남> 너 생리했냐?
여> 아니 오늘 밤새워 준비해야되...
남> 그럼 내일 니꺼 복사좀 하자.
여> 다 되면 빌려줄께...
주위 사람들... 거의 경악을 넘어선 공포 수준...
어떤 사람은 혀끝을 차고, 한숨을 쉬고...
생명공학과 대학생 세포생리학 시험준비 중인데.....
생명공학과 학생이라면 누구나 한번쯤 경험이 있을것~
[즐 = 1.57]

[공대생 사고회로]

[TTL]
'TTL'이 몰까..?...
Twenty's Life 스무살의 자유...?...
전기회로나 전자회로를 본 사람이라면..아래와 같이 생각을
Transister Transister Logic....
정보통신쪽에서는 또다른 TTL(Time To Live)..이 존재..
Through-The-Lens 렌즈를 통과한 빛의 양을 재는 노출 방식..
[삶과 죽음의 동일성]
증명) 흔히 싸우다가 보면 '반죽여버린다'는 말을 쓴다.
반죽음 = 1/2 죽음 = 1/2 삶
양변에 2를 곱한다.
죽음=삶.
[여성은 언제까지 남자의 프로포즈를 튕길 수 있는가]
이 글은 확률과정론 및 랜덤변수이론을 알아야 이해가능한 개그이다.
상황 설정은 이러하다.
한 여성에게 100명의 남자가 순차적으로 프로포즈 한다고 하자.
100명 중 백마탄 왕자는 한명 뿐이고, 여성는 그 남자를 찾고 싶어한다.
물론 그가 첫번째로 프로포즈할지 100번째로 프로포즈를 해 올지는 알 수 없을
것이다.
여자가 100명의 남자 중 제일 멋진 남자를 고른다는 건 너무 불공평하니까
한번 프로포즈한 남자를 튕기면 다시는 그 남자는 선택할 수 없다고 하자.
즉 만약 더 나은 남자가 있을 거라는 기대감에 99명의 남자를 차례로 튕겨버렸다면
100번째 프로포즈하는 남자와 결혼하는 수 밖에 없다.
물론 첫번째 남자의 프로포즈를 받아드리면 99명의 남자가 어떤 남자인지 보지도
못한다.
그러면 여자에게는 전략이 필요하다.
<몇명까지는 일단 튕겨보고 그 다음부터 만나는 남자 중 제일 멋진 남자와
결혼하자.>
여자에게 몇명까지 튕겨보는게 가장 합리적인 전략이 될까?
조건부 확률을 생각해 볼 수 있다.
B : 여자가 백마탄 왕자를 정확하게 선택할 확률.
A1 : 백마탄 왕자가 첫번째로 프로포즈해올 확률.
A2 : 백마탄 왕자가 두번째로 프로포즈해올 확률.
.
.
.
A100 : 백마탄 왕자가 백번째로 프로포즈해올 확률.
그러면 여자가 백마탄 왕자를 정확하게 선택할 확률은 다음과 같이 표현된다.
P(B) = P(A1)*P(B/A1) + P(A2)*P(B/A2) + ... +P(A100)P(B/A100) ----(1)
이제 우리의 여성이 r명까지는 일단 튕겨보고
그 다음부터 만나는 남자 중 제일 멋진 남자와 결혼하기로 했다고 하자.
그러면 P(B/A1)=0, P(B/A2)=0, ..... , P(B/Ar)=0 이다.
(당연히...최초r명 안에 백마탄 왕자가 있었다면, r명까지는 튕기기로 한 여자의
작전은 완전...실패당.)
P(B/A(r+1))=1=r/r
(당연히 r+1번째로 백마탄 왕자가 프로포즈 해 왔다면 r명까지 튕긴 여자는 이전에
본 r명보다 더 멋진 남자를 바로 만나버린 거니까 백마탄 왕자 픽업할 확률은
100%?)
P(B/A(r+2))=r/(r+1)
P(B/A(r+3))=r/(r+2)
...
P(B/A(99))=r/99
P(B/A(100))=r/100
r+2번째에 백마탄 왕자가 있는데 r+1번째 프로포즈 한 남자가 이전에 튕긴 r명보다
나은 남자였다면, 여자는 최초세운 전략상 그냥 r+1번째 남자의 프로포즈를
받아들이게
되고 그러면 r+2번째 남자는 보지도 못하니까, 여자의 입장에서는 또 전략상
실패다.
따라서 r+2번째 남자(백마탄 왕자)의 프로포즈를 받기 위해서는 r+1번째 남자가
이미 튕겨보낸
r명보다 나은 남자여서는 안될 것이다. (^^;;;)
다시 말해
백마탄 왕자보다 앞서서 프로포즈 하는 남자중 가장 괜찮은 남자가
r번째이전(r번째 포함)에 여자에게 프로포즈를 하면 된다.
r+1번째에만 있지 않으면 된다. <-- 이 부분이 매우 중요하군요!
1,2,3,...,r,r+1번째 중 r+1번째만 아니면 되니까 확률은 r/(r+1)이다.
같은 방식으로 백마탄 왕자가 r+3번째로 프로포즈를 한다면
r+1번째 r+2번째에 여자가 프로포즈를 받아들여버리면 안된다.
그러려면 백마탄 왕자 이전의 남자들 중 가장 멋진 남자가
r번재 이전(r번째 포함)에 있으면 된다.
그러면 r+1번째, r+2번째 남자가 r번째까지의 남자보다 멋질 수 없으므로
여성는 r+3번째 남자가 어떤 남자인지 살필 기회를 갖게 된다.
확률은 r/(r+2)
이런 식으로 동일 한 풀이 과정을 거치면 백마탄 왕자가 백번째로 프로포즈 해올때
여자가 백번까지 기다려서 그 왕자를 선택할 확률은 r/100
이 결과를 (1)식에 대입하면
..100....1.......r
sigma --- * ---
..x=r..100.......x
이것이다! 드디어 r에 관한 함수가 나왔다.
항수가 많으니까 그냥 연속적으로 생각해서 적분을 하자.
.......................1.......r
integral r->100 --- * --- dx
......................100......x
...r.........100
= --- [lnx]
..100........r
어차피 우리는 위의 값을 최대로 만드는 r값을 찾는거니까, 그리고 상수항과
계수는
신경 안써도 되니까
d
--[ r{ln100} - r {ln r } ]= 0 을 만드는 r을 찾자.
dr
(답)
r = 37
답이 나왔다. 37명이다.
보통 한 여자에게 프로포즈하는 남자의 숫자가 10명이라고 하면
여자는 최초 3명까지는 튕겨볼 수 있어도 4명부터는 튕겨서는 안된다는 계산이
나온다.
그냥 괜찮다 싶으면 잡아야 된다는 것이다.
솔직히 10명도 많다.
보통 여성에게 프로포즈 하는 남자가 5명쯤 된다면 최초 한명 쯤은 공주병
환자처럼 튕겨볼 수 있으나
두번째 남자가 프로포즈해올 경우...
첫번째 남자보다 낫기만 하다면 프로포즈를 받아들여야 한다는 것이다. 그만
튕기고...
[공대생 테스트]
당신은 뼛속까지 공돌이가 아닌가요???
아니라구요???
그럼 다음 단어의 뜻은 무엇일까요?
probability
equation
evaluate
frequency
function
페이지를 넘기지 말고 잠시 생각을.
...
probability - 확률
equation - 방정식 등식
evaluate - 계산하다
frequency - 주파수
function - 함수
라고 생각하신분 그대는 뼛속까지 공돌이 =ㅅ=...
실제로 사전을 찾아보면
probability : 실제로 있음직함, 개연성, 일어남직함.
equation : 평균화, 동일화, 동등화, 균일화, 평형.
evaluate : 평가하다, 견적하다.
frequency : 자주 일어나기, 빈발, 빈번.
function : 기능, 작용, 효용, 직무, 구실.
억울하다구요?
그럼 "정의" 가 영어로 뭘까요
...
definition 이라고 생각한 당신은
역시나 공돌이=_=
justice 라고 생각하신 당신은 -
문돌이 -_-;
하나 더~~~~~
어디서 주워들은 이야기입니다...
그럼 다음 단어의 뜻은 무엇일까요?
critical function..
...
임계 함수?
라고 생각하신분 그대는 뼛속까지 공돌이 =ㅅ=...
사회과학쪽 전공 서적에서는.........
비판적인 기능...
[미분과 적분에 관련된 이야기 : 미분귀신 / 적분귀신]
옛날에 아주 아름답고 평온한 마을이 있었다.
그 마을의 이름은 자연수 마을. 즉 natural number village였다.
그런데 어느날 마을에 미분 귀신이 나타났다.
미분 귀신은 마을 사람들을 하나씩 미분시켜서 모조리 0으로 만들었다.
마을은 점점 황폐해가고 이를 보다 못한 촌장과 동네사람들이 반상회를 개최하였다.
몇 시간의 토론 끝에 이웃에 있는 방정식 마을에 구원을 요청하기로 하였다.
이웃마을의 소식을 들은 마을에서는 x^2장군을 자연수 마을에 급파하였다.
전투 시에 수시로 자신의 모습을 바꾸는 x^2장군 앞에서 잠시 당황한 미분귀신...
그러나 미분귀신은 잠시 생각하더니 3번의 미분을 통해서 간단히 해치우고 말았다.
그러자 방정식 마을에서는 x^3장군을 급파하였다.
그러나 그 역시 미분 귀신의 적수가 되기엔 역부족이었다.
단 4번의 미분에 그만 작살이 나고야 말았다.
당황한 방정식 마을에서는 x^n참모총장마저 보내는 초강수를 택하였으나
그 역시 n+1 번의 미분 앞에서 힘없이 무너지고 말았다.
이제 아무도 미분 귀신의 적수가 될 수 없으리라 생각했으나....
방정식 나라에는 마지막 희망 sinx,cosx 두 장군이 있었다.
좌 sinx, 우 cosx 장군이 미분 귀신과 전투를 시작하였다.
미분 귀신은 적잖이 당황하지 않을 수 없었다.
아무리 미분을 하여도 서로 모습만 바꿔가며 계속 덤비는
sinx, cosx 장군 앞에서 더 이상 싸울 힘이 없었다.
그러나 그 순간 미분 귀신은 꾀를 내어 cosx 장군을 미분시켜 sinx 장군에게 던져버린 것이다.
마지막 희망이었던 두 장군은 서로 부디쳐서 그만 자폭하고 말았다.
일이 이쯤 되자 방정식 마을에서는 용병을 구하느라 난리가 일고 있었다.
그런데 전설적인 용병이 등장하였다. 그의 이름은 바로 exponential 검신이었다.
그가 가진 e^x 라는 무기는 미분
귀신이 수백번의 미분을해도 전혀 손상되지 않았기 때문이다.
미분귀신은 당황하기 시작하였다.
이제 승리는 exponential의 것처럼 보였다.
하지만 끝내 그마저 미분 귀신에게 패하고 말았다.
글쎄....
그 미분귀신이...
y 로 편미분을 해버리고 말았던 것이다...
우리의 미분귀신이 exponential함수 e^x를 죽이고 미분에 싫증을 느낀 나머지 자연수 나라를 떠났다.
마침내 평화가 찾아온 자연수 나라.. 그러나, 아....! 평화란 지속될 수 없는가?
이번에는 이 나라에 적분귀신이 나타나 자연수들을 닥치는 대로 적분을 시작했다!
적분귀신은 자연수들을 적분해 쓸데없이 덩치를 키워버리는가 하면,
출처가 불분명한 C(적분상수)라는 것들을 대량으로 만들어내었고,
심지어는 x로 적분한뒤 다시 y로 적분해 xy라는 악질 돌연변이까지 만들어 내는 것이었다
이제야 평화가 오는가 했던 자연수 나라의 촌장은 아연실색을 하며
옆 마을 다항식의 나라에 도움을 청했다. 그러나 다항식의 나라는
적분귀신은 자국에 도움이 된다며 이를 거절했다. 심지어 '적분귀신을 환영합니다'
라는 플랭카드를 내걸기도 하였다. 자연수왕은 얼마 안 남은 순수 자연수들을 모아
대책회의를 열었다. 회의 결과 다시 미분귀신을 불러야 한다는 의견이 나왔다.
그러나 미분귀신을 부르면 그들조차 막대한 피해가 있기에 그들 사이에서도 의견이 분분했다.
결국 미분귀신을 부른 후 순수 자연수들만 비밀 아지트에 숨기로 하고 미분귀신을 불렀다.
다시 자연수 마을에 온 미분귀신..!
일단 상수 C들을 닥치는 대로 죽이고, 다항식들을 죽이기 시작했다.
거의 모든 다항식들이 죽어갈 무렵, 미분귀신 앞에 적분귀신이 나타났다.
적분귀신 "문제를 내어 이기는 쪽이 사라지도록 하자"
미분귀신 "좋다(흐흐.. 내겐 편미분이라는 무기가..)"
그.러.나...
적분귀신이 문제로 제시한 것은 무한다변수 다항식
Lim a1*a2*....*an 이었다.
n->∽
아무리 편미분을 해 봐도 끊임없이 쏟아지는 변수들..
미분귀신 "포기다.. 너의 솜씨를 보여다오..-_-;;"
적분귀신 "가소로운 것.. 에잇!"
눈앞의 무한다변수다항식이 흔적도 없이 소멸되어버리는 것이 아닌가...
미분귀신 "어.. 어떻게?-_-;;;"
적분귀신 "......."
그렇다...
적분귀신은 다항식을 0에서 0까지 정적분해 버렸던 것이다...
적분귀신은 정말 대단했다.
승승장구를 치던 적분귀신에게 대적할만한 상대가 자연수 마을에서는 더이상 존재하지 않았다.
여지없이 무너진 미분귀신은 함께 힘을 합하여 적분귀신을 물리칠 동지를 찾아 나섰다.
정수마을, 유리수마을, 실수마을, 심지어 그 복잡하다는 복소수(complex number)마을까지...
그러나 미분귀신은 더이상 동지를 찾을 수 없는듯 했다.
"수의 마을에서는 도저히 찾을 수 없는것인가?..."
자포자기한 미분귀신 앞에 펼쳐진 광경은 정말 놀라운 광경이었다.
실수 및 복소수 마을에서 continuous function들이
어떤 놈에게 여지없이 터져서는 산산 조각이 나는 것이었다.
"저놈이닷!" 미분귀신이 외쳤다.
자세히 보니 그놈은 delta function 였다.
연속함수들을 sampling을 통해 discrete function으로 만들고 있었던 것이다.
며칠 후...
자연수 마을로 돌아온 미분귀신은 델타함수를 적분귀신 앞에 내놓았다.
적분귀신은 자신의 비장의 무기인 0에서 0까지 정적분을 사용했다.
그러나 delta function은 사라지지 않고 1을 남겼다.
delta function은 정말 대단했다.
특이하게도 0(-0)에서 0(+0)까지 정적분을 하면 1이되는 것이었다.
순간 당황한 적분귀신은 정신을 가다듬고 다시 0에서 0까지 정적분을 시도했다.
그러자 1이 사라졌다.
이때 나선 미분귀신은 delta function을 무한번 미분해주기 시작했다.
적분귀신이 아무리 아무리 0에서 0까지 정적분을 시도해도
미분을 통해 계속 delta function의 변종들이 나타나는 것이었다.
적분귀신은 드디어 두손두발, 아니 두 인티그랄(integral)을 다 들고 말았다.
미분귀신과 delta function의 연합전선은 정말 대단했다.
그러나 잠시잠깐 그들이 한눈을 판 사이에
그들은 사라지고 말았다.
"무슨일이지...?" 적분귀신이 고개를 들었다.
...
...
...
그 거대한 못짓.
그는 말 한마디로 모든 것을 사라지게 할 수 있는
거의 신적인 존재였다.
그는 바로 '정의(definition)귀신'이었다.
미분귀신과 델타함수가 열심히 ally를 해도
마지막에 정의귀신이 "= 0" 한마디면 끝나는 것이었다.
과연 정의귀신을 대적할 자가 이세상에 존재할른지...
존재한다. 바로 정의귀신을 창조한 미분위상수학대박사. 그러나 정의귀신은 미분위상수학대박사에게 광신적으로 충성하기 때문에 서로 싸우는 일은 없다. 단지 미분위상수학대박사가 정의귀신보다 훨씬 전지전능함을 말하려는 목적에서 언급한 것이다.



