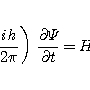제라툴 : 흠. 대략 이러한 내용들이군요.

벨제뷔트 사탄(pccm) : 조금 긴 내용이지. 내가 이러한 내용을 설명하고자 함은 물론 양자역학적인 스킬의 본질을 알려주기 위함이지. 그리고 또한 중요한 사악함의 법칙을 아는 일에도 필요한 내용일세.

테사더 : 대체 무슨 내용이길레??

벨제뷔트 사탄(pccm) : 카오스적이면서도 물리학적인 내용인 엔트로피 법칙(entropy principle)이지.

제라툴 : ???

벨제뷔트 사탄(pccm) : 이해가 잘 안될걸. 쉽게 말하자면 무질서의 정도를 측정한 값이지.

제라툴 : ???(더욱 이해가 안되는 표정을 하며)

벨제뷔트 사탄(pccm) : 우선 다음글을 보도록.

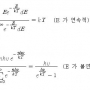
1865년 R.E.클라우지우스가 변화를 뜻하는 그리스어 τροπη에서 이 물리량을 엔트로피라 이름하였다. 이론적으로는 물질계가 흡수하는 열량 dQ와 절대온도 T와의 비 dS=dQ/T로 정의한다. 여기서 dS는 물질계가 열을 흡수하는 동안의 엔트로피 변화량이다. 열기관의 효율을 이론적으로 계산하는 이상기관의 경우는 모든 과정이 가역과정이므로 엔트로피는 일정하게 유지된다. 일반적으로 현상이 비가역과정인 자연적 과정을 따르는 경우에는 이 양이 증가하고, 자연적 과정에 역행하는 경우에는 감소하는 성질이 있다. 그러므로 자연현상의 변화가 자연적 방향을 따라 발생하는가를 나타내는 척도이다.

대부분 자연현상의 변화는 어떤 일정한 방향으로만 진행한다. 즉, 자연현상의 변화는 물질계의 엔트로피가 증가하는 방향으로 진행한다. 이것을 엔트로피 증가의 법칙이라고 한다. 예를 들면, 온도차가 있는 어떤 2개의 물체를 접촉시켰을 때, 열 q가 고온부에서 저온부로 흐른다고 하면 고온부(온도 T1)의 엔트로피는 q/T1만큼 감소하고, 저온부(온도 T2)의 엔트로피는 q/T2만큼 증가하므로, 전체의 엔트로피는 이 변화를 통하여 증가한다. 역으로 저온부에서 고온부로 열이 이동하는 자연현상에 역행하는 과정, 예를 들면 냉동기의 저온부에서 열을 빼앗아 고온부로 방출하는 과정에서 국부적으로 엔트로피가 감소하지만, 여기에는 냉동기를 작동시키는 모터 내에서 전류가 열로 바뀐다는 자연적 과정이 필연적으로 동반하므로 전체로서는 엔트로피가 증가한다. 때때로 자연현상은 국부적으로 엔트로피가 감소하는 비자연적 변화를 따르는 것도 있지만, 그것에 관계되는 물질계 전체를 다루어 보면, 항상 엔트로피를 증가시키는 방향으로 현상이 변화한다. 이 이론은 자연현상이 일어나는 방향을 정하는 것으로서, 에너지보존법칙과 함께 열역학의 기본법칙으로서 중요하다. 이상기체에서 엔트로피가 증가하지 않는 것은 가역변화라고 하는 비현실적인 변화를 가정하고 있기 때문이다.

엔트로피는 물질계의 열적 상태로부터 정해진 양으로서, 통계역학의 입장에서 보면 열역학적인 확률을 나타내는 양이다. 엔트로피 증가의 원리는 분자운동이 확률이 적은 질서 있는 상태로부터 확률이 큰 무질서한 상태로 이동해 가는 자연현상으로 해석한다. 예를 들면, 마찰에 의해 열이 발생하는 것은 역학적 운동(분자의 질서 있는 운동)이 열운동(무질서한 분자운동)으로 변하는 과정이다. 그 반대의 과정은 무질서에서 질서로 옮겨가는 과정이며, 이것은 자발적으로 일어나지 않는다.

일반적으로 열역학적 확률의 최대값은 온도가 균일한 열평형상태에 대응하는 것이다. 고찰하고 있는 물질계가 다른 에너지 출입이 없는 고립계인 경우에는 늦던 빠르던 전체가 열평형에 도달하여 모든 열과정이 정지하는 것이라고 생각된다. 이로부터 엔트로피 증가의 법칙이 발표된 직후 만약 이 법칙이 정당하다면 우주는 어느 것이나 열평형에 도달하여 모든 종류의 에너지가 분자의 불규칙적인 열운동으로 변하여, 열의 종말, 즉 우주의 종말에 도달하게 될 것이라는 논쟁이 있었다. 그러나 이는 우주를 고립된 유한한 계라고 가정했을 때의 결론이다.

즉 결론적으로 내가 말하다면. 이 엔트로피를 증가시킨다면 이 세상은 혼돈, 즉 카오스로 되겠지. 우리가 하는 모든 일들도 다 엔트로피가 증가하는 방향이 되지. 이것을 열역학 제2 법칙의 클라지우스 표현이라고 한단다. 모든 자연현상들은 엔트로피가 증가하는 방향으로 흘러가지. 우주는 유한한 계(系)가 되지. 무한하게 보일지는 모르나 우주는 3~4차원 구면이야. 이 구면의 호몰로지군이나 호모토피군은 잘 알려진 바와같이 정수전체의 집합인 정수환 Z가 되지. (대수적 위상수학에서 말하는 흔한 정리인 서스펜션의 정리로 된다.) 구면이라는 다양체는 성질이 특이하지. 같은 차원이 아니면 거의 0의 값을 호모토피군이 취하지(물론 0차원 호몰로지군은 무조건 정수환 Z) 또한 미분기하학에서는 곡률이 구면의 반지름의 제곱의 역수가 되지. 또한 가우스-보네 정리에서 구면의 위상기하적인 성질도 간단하지.

지옥의 화염을 사용하는일도 열의 변화량인 dQ를 증가시키는 일이지. 결론적으로 말해서 이거 역시 엔트로피를 증가시키며 카오스화를 가속화시키지. 자연상태는 점점 무질서해지며 자연재해도 더욱 거세어지지. 간단한 예로 베이징에서의 나비의 날개짓이 미국 뉴욕에서의 허리케인을 유도할수도 있어.

제라툴 : 통계역학에서 대표적으로 사용하는 분포(distribution)가 뭐죠?

벨제뷔트 사탄(pccm) : 맥스웰-볼츠만 속력분포(maxwell-boltzman velocity distribution)이지. 이러한 속력분포는 기체분자의 성분에 따라서 달라지지. 그렇지만 한가지 분명한건 이 속력분포를 0에서 무한대까지 적분하면 1이 되는 사실이지. 그러니깐 확률분포라는 이름이 붙게 되는거지.

제라툴 : 그렇군요.

벨제뷔트 사탄(pccm) : 또한 양자역학에서 보면 어떠한 입자의 고유한 파동함수가 존재하지. 물론 이것도 일정한 영역을 잡아놓아야 하고 상수를 규격화 시켜야먄 하지. 이 파동함수는 특별한 양자역학의 방정식인 슈뢰딩거 방정식을 만족하지.

L.V.드브로이의 물질파(物質波) 개념에 대해 영향을 받아 1926년 슈뢰딩거가 미시적 역학계의 양자화(量子化) 문제를 편미분방정식의 고유값 문제로 취급하기 위하여 유도한 방정식이다. 이 방정식에 의하면 원자 안에 있는 전자가 궤도 내에 남아있는 한 빛을 방출하지 않는다. 이 정상파에 대한 생각은 가속도로 원운동을 하고 있는 전자파에 대한 생각을 바꾸어 놓았다. 이 방정식에 의하면 물질의 존재형태는 파동으로 기술할 수 있다. 입자의 존재 자체를 완벽하게 기술할 수 있는 확률은 시간에 따라 변화하는데, 변화하는 양상은 파동과 비슷하다. 이것을 기술할 수 있는 방정식이 슈뢰딩거의 파동방정식이다. 슈뢰딩거가 물질의 운동에 대한 새로운 이론인 파동방정식을 발표함에 따라서 물리학은 수학적인 구조에 있어서 크게 발전했다. 원자에 대한 하나의 상을 제공했기 때문이다.

결국 양자역학은 1925년 W.K.하이젠베르크가 제안한 행렬역학(行列力學)과 1926년 슈뢰딩거가 발전시킨 파동역학을 중심으로 하여 완성되었다고 할 수 있다. 양자역학에 따르면 모든 물질은 입자성과 동시에 파동성을 가지므로 파동방정식을 만족하는 파동함수 Ψ(x, t)에 의하여 입자의 상태가 확률로서 결정된다. 슈뢰딩거의 방정식은 다음과 같다.




h는 플랑크상수이고, H는 해밀토니안(해밀턴演算子)인데 그 고유값은 계(系)의 에너지이며, H의 함수형은 구체적인 문제에 따라 대응원리(對應原理)로부터 고전물리학을 모델로 하여 결정된다.

참고로 대응원리란 양자역학의 운동법칙의 부분적인 법칙이 바로 거시세계의 운동법칙이라는 원리이지. 해밀토니안은 고전역학에서도 많이 나오는 개념이야. 라그랑지안도 마찬가지이지. 뉴튼의 제2 법칙인 힘과 가속도의 법칙은 라그랑지안이나 해밀토니안으로 표시되는것이 가능해.

위의 슈뢰딩거 방정식의 규격화된 해는 곧 입자의 파동함수가 되지. 이 파동함수의 절대값의 제곱이 바로 그 입자의 확률분포야. 간단한 예로는 오비탈(orbital)이 있지. 전자의 확률적인 분포를 표현한 개념이라고 알아두면 편할거야.

또한 W.K. 하이젠베르크(W.K.heigenberg)의 불확정성 원리가 있지.

지금까지 말한 내용은 극히 일부분에 지나지 않아. 그러나 이 내용으로 수많은 정술이나 스킬들을 만들수있어. 특히 카오스의 법칙은 매우 중요하지. 꼭 배워두는게 좋아. 테사더 너가 쓰는 사이오닉 스톰도 일종의 카오스 법칙으로 인한 마법이지만 좀더 구체적으로 강화시키는것이 중요해. 다음 기본적인 사실을 꼭 알아두도록.



지금 우리가 쓰는 단순한 스킬들


(예를들어 사이오닉 스톰이)이 리아라를 죽

이는


다크니스를 불러올수 있다.