Zeeman Interaction
An external magnetic field will exert a torque on a magnetic dipole and the magnetic potential energy which results is
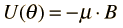
The magnetic dipole moment associated with the orbital angular momentum is given by
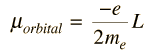
For magnetic field in the z-direction this gives
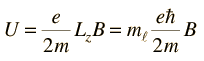
Considering the quantization of angular momentum , this gives equally spaced energy levels displaced from the zero field level by
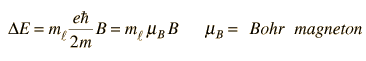
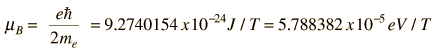
This displacement of the energy levels gives the uniformly spaced multiplet splitting of the spectral lines which is called the Zeeman effect.
The magnetic field also interacts with the electron spin magnetic moment, so it contributes to the Zeeman effect in many cases. The electron spin had not been discovered at the time of Zeeman's original experiments, so the cases where it contributed were considered to be anomalous. The term "anomalous Zeeman effect" has persisted for the cases where spin contributes. In general, both orbital and spin moments are involved, and the Zeeman interaction takes the form
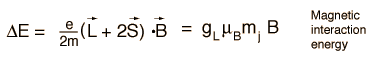
The factor of two multiplying the electron spin angular momentum comes from the fact that it is twice as effective in producing magnetic moment. This factor is called the spin g-factor or gyromagnetic ratio. The evaluation of the scalar product between the angular momenta and the magnetic field here is complicated by the fact that the S and L vectors are both precessing around the magnetic field and are not in general in the same direction. The persistent early spectroscopists worked out a way to calculate the effect of the directions. The resulting geometric factor gL in the final expression above is called the Lande g factor. It allowed them to express the resultant splittings of the spectral lines in terms of the z-component of the total angular momentum, mj.
The above treatment of the Zeeman effect describes the phenomenon when the magnetic fields are small enough that the orbital and spin angular momenta can be considered to be coupled. For extremely strong magnetic fields this coupling is broken and another approach must be taken. The strong field effect is called the Paschen-Back effect.

 음악도
음악도